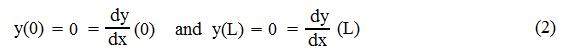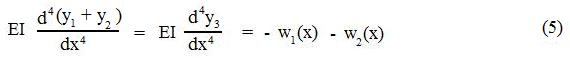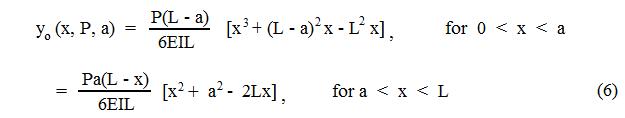Where to Find a Continuous Beam Analysis Spreadsheet
To obtain a continuous beam analysis spreadsheet, Click Here to go to our spreadsheet store. Also, check out our Free Android App for analyzing a simply supported beam with a concentrated load. Read on for information about performing continuous beam analyses via superposition and how Excel spreadsheets can be used in this procedure.
The equation giving the deflection of a beam with a complicated loading can often be found relatively easily by superposing two or more deflection equations corresponding to simple loadings. Superposition can be used, however, only if the beam deflections are small, say less than 1/500-th of the beam span. Fortunately the vast majority of beams designed by structural and mechanical engineers involve deflections this small or smaller, and thus superposition is applicable to a wide range of practical problems.
Background on Superposition in a Continuous Beam Analysis Spreadsheet
The theoretical justification for superposition is straightforward. Consider the differential equation for beam deflection, y(x)
in which w(x) is the load acting on the beam, E isthe elastic modulus of the beam material, I is the moment of inertia of the cross section, and x is a horizontal coordinate, measured from the left end and locating points on the beam. The deflection function y(x) must satisfy Eq. 1 and also the boundary conditions. For example, for a beam fixed at both ends, the boundary conditions would be
in which L is the length of the beam.
Now suppose that a load w1(x) acts on the beam. Then the deflection y1(x) of the beam is governed by Eq.1:
Next, remove the load w1(x) and apply a different load, w2(x). Then the deflection y2(x) of the beam is also governed by Eq.1:
Adding Eqs. 3 and 4 and defining a new function, y3(x) ≡ y1(x) + y2(x), gives
In words, y3(x) satisfies the differential equation for a beam subjected to the combined loading, w1(x) plus w2(x), and, furthermore, y3(x) can be found by simply adding the deflection equations corresponding to w1(x) and w2(x) acting alone (Note that boundary conditions, such as Eq. 2, also are satisfied after superposition).
So why bother with superposition? Why not just solve Eq. 5 directly for y3(x)? Answer: Superposition is in fact not worth bothering about, unless tabulated solutions exist for y1(x) and y2(x). Because if someone else has already solved the differential equations for y1(x) and y2(x) (and the solutions are available to you, typically through a published table of solutions) then all you have to do is add their results—you completely avoid the time-consuming, error-prone process of solving the differential equation for y3(x).
Example Calculations with Beam Formulas
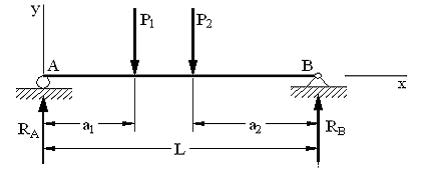
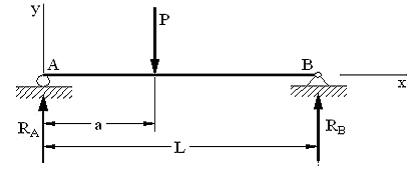
As an illustration, consider the beam shown in the figure below.
For concreteness, let a1 = 2 m, a2 = 3 m, L = 12 m, P1 = 10 kN, P2 = 14 kN, E = 200 GPa, and I = 600 000 cm4.
The general result for a single load is given by equation (6) below, which is found in all tables of beam deflection formulas:
The deflection equation is
This equation can be used to give the deflection equation y(x) for our two-load problem through superposition
y(x) = yo(x, 10 kN, 2 m) + yo(x, 14 kN, 9 m) (7)
That is, we apply Eq. 6 twice, once for the 10-kN load acting a = 2 m from the left end, and once for the 14-kN load acting a = 12 m − 3 m = 9 m from the left end.
The forms of Eqs. 6 and 7 are well-suited for implementation in a spreadsheet. We only have to program a single formula (with an “If” statement) representing Eq. 6, and then we can superpose the results of that formula once for each concentrated load acting on the beam—no matter how many loads act or where they act. The same superposition approach can be used to calculate the shear and moment diagrams.Obviously, a similar approach can be used for other tabulated solutions, such as those corresponding to a concentrated moment or distributed load acting on the beam.
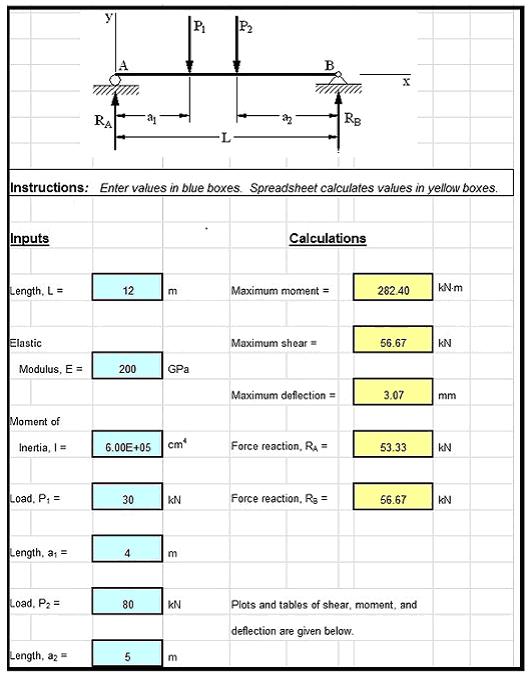
Screenshot for Continuous Beam Analysis Spreadsheet Calculations
The screenshot image below shows an Excel spreadsheet to calculate the shear and moment diagrams and deflections for two concentrated loads acting on a simply-supported beam. Note that only the absolute minimum of information is required: the magnitude and location of the loads and the values of E and I. No nodal numbering, element numbering, boundary condition specification, output specification, and load type must be entered.
The workbook of which this spreadsheet is a part contains tabs for one and two concentrated forces, one and twoconcentrated moments, one and two linearly varying distributed loads, and a combination of all three types of loadings. The procedure to extend the analysis to other load cases is also presented in a tab. Because all formulas used in each tab are visible and can be unlocked, userspossessing only a basic knowledge of Excel may easily customize the spreadsheet to meet particular needs and recurrent applications. This Excel workbook and additional workbooksfor other boundary conditions are available in either U.S. or S.I. units at low cost in our spreadsheet store.
References
1. Manual of Steel Construction, Load & Resistance Factor Design, Volume I, Structural Members, Specifications & Codes, 2nd Edition, American Institute of Steel Construction, Chicago, IL, American Institute of Steel Construction (1994).
2. Egor P. Popov, Engineering Mechanics of Solids, 2nd Edition, Prentice Hall, New York, NY (1998).
3. Rossow, Mark, “Structural Analysis of Beams Spreadsheets,” an online blog article