Category Archives: Manning Equation/Open Channel Flow

articles on use of Excel spreadsheets for Manning equation calculations with open channel flow

Manning Equation Open Channel Flow Calculator Excel Spreadsheets

Posted on by
Reply

Where to Find a Manning Equation Open Channel Flow Calculator Spreadsheet

To obtain a Manning equation open channel flow calculator excel spreadsheet, click here to visit our spreadsheet store.  Why use online calculators or make open channel flow/Manning Equation calculations by hand when you can buy a variety of Manning equation open channel flow calculator excel spreadsheets or spreadsheet packages for prices ranging from $6.95 to $27.95?  Read on for information about Excel spreadsheets that can be used as a Manning equation open channel flow calculator.

picture for a Manning equation open channel flow calculatorAn excel spreadsheet can conveniently be used as a Manning equation open channel flow calculator.  The Manning equation can be used for water flow rate calculations in either natural or man made open channels.  Uniform open channel flow calculations with the Manning equation use the channel slope, hydraulic radius,  flow depth, flow rate, and Manning roughness coefficient.   Image Credit: geograph.org.uk

Uniform Flow for a Manning Equation Open Channel Flow Excel Spreadsheet

Diagram for a Manning Equation Open Channel Flow Calculator Spreadsheet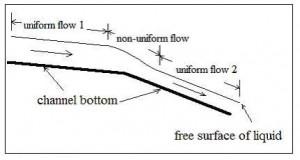Open channel flow may be either uniform flow or nonuniform flow, as illustrated in the diagram at the left.  For uniform flow in an open channel, there is always a constant volumetric flow of liquid through a reach of channel with a constant bottom slope, surface roughness, and hydraulic radius (that is constant channel size and shape).  For the constant channel conditions described, the water will flow at a constant depth (usually called the normal depth) for the  particular volumetric flow rate and channel conditions. The diagram above shows a stretch of uniform open channel flow, followed by a change in bottom slope that causes non-uniform flow, followed by another reach of uniform open channel flow.  The Manning Equation, which will be discussed in the next section, can be used only for uniform open channel flow.

Equation and Parameters for a Manning Equation Open Channel Flow Calculator Excel Spreadsheet

The Manning Equation is:

Q = (1.49/n)A(R2/3)(S1/2) for the U.S. units shown below, and it is:

Q = (1.0/n)A(R2/3)(S1/2) for the S.I. units shown below.

  • Q is the volumetric water flow rate in the reach of channel (ft3/sec for U.S.) (m3/s for S.I.)
  • A is the cross-sectional area of flow  (ft2for U.S.) (m2for S.I.)
  • P is the wetted perimeter of the flow  (ft for U.S.)  (m for S.I.)
  • R is the hydraulic radius, which equalsA/P(ft for U.S.) (m for S.I.)
  • S is the bottom slope of the channel, (dimensionless or ft/ft -U.S. & m/m – S.I.)
  • n is the empirical Manning roughness coefficient, which is dimensionless

The equation V = Q/A, a definition for average flow velocity, can be used to express the Manning Equation in terms of average flow velocity,V, instead of flow rate,Q, as follows:

V = (1.49/n)(R2/3)(S1/2) for U.S. units with V expressed in ft/sec.

Or V = (1.0/n)(R2/3)(S1/2) for S.I. units with V expressed in m/s.

It should be noted that the Manning Equation is an empirical equation.  The U.S. units must be just as shown above for use in the equation with the constant 1.49 and the S.I. units must be just as shown above for use in the equation with the constant 1.0.

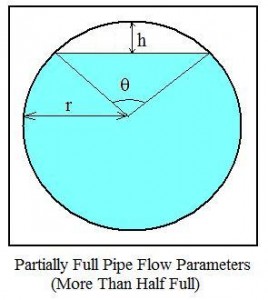
The Manning Roughness Coefficient for a Manning Equation Open Channel Flow Calculator Excel Spreadsheet

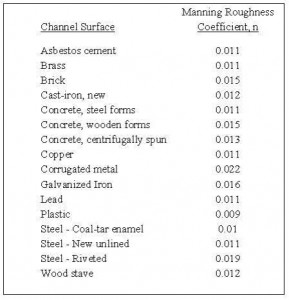Manning Equation Open Channel Flow Calculator Manning Roughness CoefficientsAll calculations with the Manning equation (except for experimental determination of n) require a value for the Manning roughness coefficient, n, for the channel surface.  This coefficient, n, is an experimentally determined constant that depends upon the nature of the channel and its surface.  Smoother surfaces have generally lower Manning roughness coefficient values and rougher surfaces have higher values. Many handbooks, textbooks and online sources have tables that give values of n for different natural and man made channel types and surfaces. The table at the right gives values of the Manning roughness coefficient for several common open channel flow surfaces for use in a Manning equation open channel flow calculator excel spreadsheet.

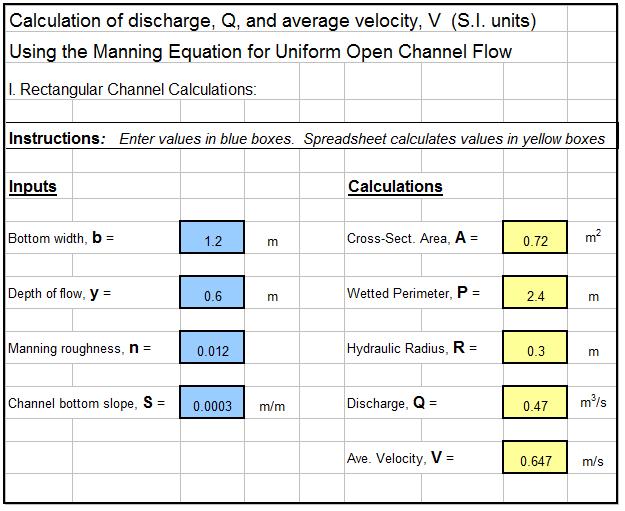
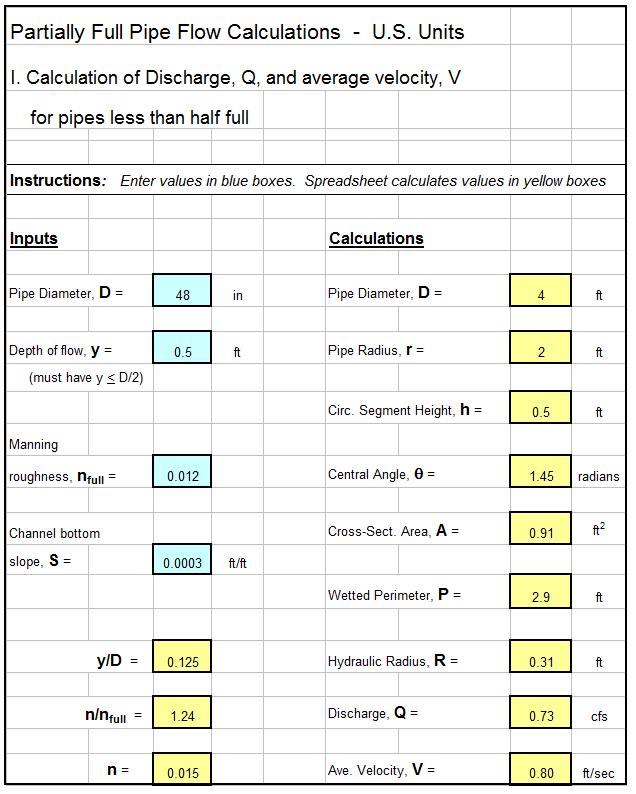
Example Manning Equation Open Channel Flow Excel Spreadsheet

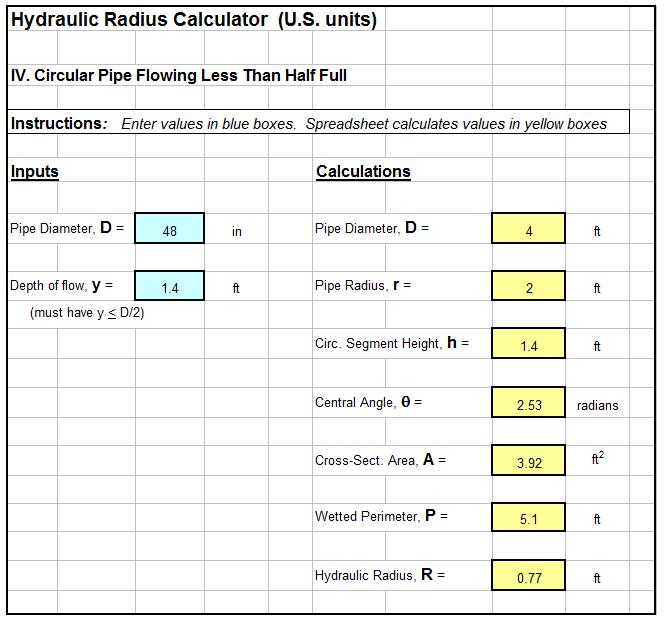
The Manning equation open channel flow calculator excel spreadsheet shown in the image below can be used to calculate flow rate and average velocity in a rectangular open channel with specified channel width, bottom slope, & Manning roughness, along with the flow rate through the channel.  This Excel spreadsheet and others for Manning equation open channel flow calculations for rectangular, trapezoidal or triangular channels, in either U.S. or S.I. units are available for very reasonable prices in our spreadsheet store.

Manning Equation Open Channel Flow Calculator Excel Spreadsheet

References

1. Bengtson, Harlan H., Open Channel Flow I – The Manning Equation and Uniform Flow, an online, continuing education course for PDH credit.

2. U.S. Dept. of the Interior, Bureau of Reclamation, 2001 revised, 1997 third edition, Water Measurement Manual.

3. Chow, V. T., Open Channel Hydraulics, New York: McGraw-Hill, 1959.

4.  Bengtson, Harlan H., “Manning Equation Open Channel Flow Excel Spreadsheets,”  an online blog article, 2012.

5. Bengtson, Harlan H., “The Manning Equation for Open Channel Flow Calculations“, available as an Amazon Kindle e-book and as a paperback.

Partially Full Pipe Flow Calculator with Excel Spreadsheets

Posted on by

Where to Find Partially Full Pipe Flow Calculator Spreadsheets

To obtain Excel spreadsheets for partially full pipe flow calculations, click here to visit our spreadsheet store  for partially full pipe flow calculator spreadsheets. Read on for information about Excel spreadsheets that can be used as a partially full pipe flow calculator.

The Manning equation can be used for flow in a pipe that is partially full, because the flow will be due to gravity rather than pressure.  the Manning equation [Q = (1.49/n)A(R2/3)(S1/2) for (U.S. units) or Q = (1.0/n)A(R2/3)(S1/2) for (S.I. units)] applies if the flow is uniform flow  For background on the Manning equation and open channel flow and the conditions for uniform flow, see the article, “Manning Equation/Open Channel Flow Calculations with Excel Spreadsheets.”

Graph for use with a partially full pipe flow calculatorDirect use of the Manning equation as a partially full pipe flow calculator, isn’t easy, however, because of the rather complicated set of equations for the area of flow and wetted perimeter for partially full pipe flow.  There is no simple equation for hydraulic radius as a function of flow depth and pipe diameter.  As a result graphs of Q/Qfull and V/Vfull vs y/D, like the one shown at the left are commonly used for partially full pipe flow calculations.  The parameters, Q and V in this graph are flow rate an velocity at a flow depth of y in a pipe of diameter D.  Qfull and Vfull can be conveniently calculated using the Manning equation, because the hydraulic radius for a circular pipe flowing full is simply D/4.

With the use of Excel formulas in an Excel spreadsheet, however, the rather inconvenient equations for area and wetted perimeter in partially full pipe flow become much easier to work with.  The calculations are complicated a bit by the need to consider the Manning roughness coefficient to be variable with depth of flow as discussed in the next section.

Is the Manning Roughness Coefficient Variable for Partially Full Pipe Flow Calculations?

Using the geometric/trigonometric equations discussed in the next couple of sections, it is relatively easy to calculate the cross-sectional area, wetted perimeter, and hydraulic radius for partially full pipe flow  with any specified pipe diameter and depth of flow.  If the pipe slope and Manning roughness coefficient are known, then it should be easy to calculate flow rate and velocity for the given depth of flow using the Manning Equation                             [Q = (1.49/n)A(R2/3)(S1/2)], right?   No, wrong!  As long ago as the middle of the twentieth century, it had been observed that measured flow rates in partially full pipe flow aren’t the same as those calculated as just described.  In a 1946 journal article (ref #1 below), T. R. Camp presented a method for improving the agreement between measured and calculated values for partially full pipe flow.  The method developed by Camp consisted of using a variation in Manning roughness coefficient with depth of flow as shown in the graph above.

Although this variation in Manning roughness due to depth of flow doesn’t make sense intuitively, it does work.  It is well to keep in mind that the Manning equation is an empirical equation, derived by correlating experimental results, rather than being theoretically derived.  The Manning equation was developed for flow in open channels with rectangular, trapezoidal, and similar cross-sections.  It works very well for those applications using a constant value for the Manning roughness coefficient, n.  Better agreement with experimental measurements is obtained for partially full pipe flow, however, by using the variation in Manning roughness coefficient developed by Camp and shown in the diagram above.

The graph developed by Camp and shown above appears in several publications of the American Society of Civil Engineers, the Water Pollution Control Federation, and the Water Environment Federation from 1969 through 1992, as well as in many environmental engineering textbooks (see reference list at the end of this article).  You should beware, however that there are several online calculators and websites with equations for making partially full pipe flow calculations using the Manning equation with constant Manning roughness coefficient, n.  The equations and Excel spreadsheets presented and discussed in this article use the variation in n that was developed by T.R. Camp.

Excel Spreadsheet/Partially Full Pipe Flow Calculator for Pipe Less than Half Full

Diagram to for Partially Full Pipe Flow CalculatorThe parameters used in partially full pipe flow calculations with the pipe less than half full are shown in the diagram at the right.  K is the circular segment area; S is the circular segment arc length; h is the circular segment height; r is the radius of the pipe; and θ is the central angle.

The equations below are those used, together with the Manning equation and Q = VA, in the partially full pipe flow calculator (Excel spreadsheet) for flow depth less than pipe radius, as shown below.

  • h = y
  • θ = 2 arccos[ (r – h)/r ]
  • A = K = r2(θ – sinθ)/2
  • P = S = rθ

The equations to calculate n/nfull, in terms of y/D for y < D/2 are as follows

  • n/nfull = 1 + (y/D)(1/3) for 0 < y/D < 0.03
  • n/nfull = 1.1 + (y/D – 0.03)(12/7) for 0.03 < y/D < 0.1
  • n/nfull = 1.22 + (y/D – 0.1)(0.6) for 0.1 < y/D < 0.2
  • n/nfull = 1.29 for 0.2 < y/D < 0.3
  • n/nfull = 1.29 – (y/D – 0.3)(0.2) for 0.3 < y/D < 0.5

The Excel template shown below can be used as a partially full pipe flow calculator to calculate the pipe flow rate, Q, and velocity, V, for specified values of pipe diameter, D, flow depth, y, Manning roughness for full pipe flow, nfull; and bottom slope, S, for cases where the depth of flow is less than the pipe radius.  This Excel spreadsheet and others for partially full pipe flow calculations are available in either U.S. or S.I. units at a very low cost in our spreadsheet store.

screenshot of partially full pipe flow calculator spreadsheet

Excel Spreadsheet/Partially Full Pipe Flow Calculator for Pipe More than Half Full

The parameters used in partially full pipe flow calculations with the pipe more than half full are shown in the diagram at the right.  K is the circular segment area; S is the circular segment arc length; h is the circular segment height; r is the radius of the pipe; and θ is the central angle.

The equations below are those used, together with the Manning equation and Q = VA, in the partially full pipe flow calculator (Excel spreadsheet) for flow depth more than pipe radius, as shown below.

  • h = 2r – y
  • θ = 2 arccos[ (r – h)/r ]
  • A = πr2 – K = πr2 – r2(θ – sinθ)/2
  • P = 2πr – S = 2πr – rθ

The equation used for n/nfull for 0.5 < y//D < 1 is: n/nfull = 1.25 – [(y/D – 0.5)/2]

An Excel spreadsheet like the one shown above for less than half full flow, and others for partially full pipe flow calculations, are available in either U.S. or S.I. units at a very low cost at www.engineeringexceltemplates.com.

References

1. Bengtson, Harlan H.,  Uniform Open Channel Flow and The Manning Equation, an online, continuing education course for PDH credit.

2. Camp, T.R., “Design of Sewers to Facilitate Flow,” Sewage Works Journal, 18 (3), 1946

3. Chow, V. T., Open Channel Hydraulics, New York: McGraw-Hill, 1959.

4. Steel, E.W. & McGhee, T.J., Water Supply and Sewerage, 5th Ed., New York, McGraw-Hill Book Company, 1979

5.  ASCE, 1969. Design and Construction of Sanitary and Storm Sewers, NY

6. Bengtson, H.H., “Manning Equation Partially Filled Circular Pipes,”  An online blog article

7. Bengtson, H.H., “Partially Full Pipe Flow Calculations with Spreadsheets“, available as an Amazon Kindle e-book and as a paperback.

 


 

 

 


Hydraulic Radius Open Channel Flow Excel Spreadsheets

Posted on by

Where to Find Spreadsheets for Hydraulic Radius Open Channel Flow Calculations

For an Excel spreadsheet to use for hydraulic radius open channel flow calculations, click here to visit our spreadsheet store.  Read on for information about hydraulic radius open channel flow calculations.

The hydraulic radius is an important parameter for open channel flow calculations with the Manning Equation.  Excel spreadsheets can be set up to conveniently make hydraulic radius open channel flow calculations for flow through common open channel shapes like those for a rectangular, triangular or trapezoidal flume.  Parameters like trapezoid area and perimeter and triangle area and perimeter are needed to calculate the hydraulic radius as described in the rest of this article.

The hydraulic radius for open channel flow is defined to be the cross sectional area of flow divided by the wetted perimeter.  That is: R = A/P, where A is the cross sectional area of flow, P is the portion of the cross sectional perimeter that is wetted by the flow, and R is the hydraulic radius.  The next several sections will present the equations to calculate A, P, and R for some common open channel shapes, and then discuss the use of Excel spreadsheets for hydraulic radius open channel flow calculations.

Hydraulic Radius Open Channel Flow Calculation for Rectangular Channels

hydraulic radius open channel flow diagram for rectangular channelRectangular channels are widely used for open channel flow, and hydraulic radius open channel flow calculations are quite straightforward for a rectangular cross section. The diagram at the left shows the depth of flow represented by the symbol, y, and the channel bottom width represented by the symbol, b.  It is clear from the diagram that A = by and P = 2y + b.  Thus the equation for the hydraulic radius is: R = by/(2y + b) for open channel flow through a rectangular cross section.


Hydraulic Radius Open Channel Flow Trapezoidal Flume Calculations

hydraulic radius open channel flow diagram for trapezoidal flumeThe trapezoid is probably the most common shape for open channel flow. Many man-made open channels are trapezoidal flumes, including many urban storm water arroyos in the southwestern U.S.  Also, many natural channels are approximately trapezoidal in cross section. The parameters typically used for the size and shape of a trapezoidal flume in hydraulic radius open channel flow calculations are shown in the diagram at the right. Those parameters, which are used to calculate the trapezoid area and wetted perimeter, are as follows:

  • y is the liquid depth (ft for U.S. & m for S.I.)
  • b is the bottom width of the channel (ft for U.S. & m for S.I.)
  • B is the width of the liquid surface (ft for U.S. & m for S.I.)
  • λ is the wetted length measured along the sloped side (ft for U.S. & m for S.I.)
  • α is the angle of the sloped side from vertical. The side slope also often specified as horiz:vert = z:1.

The common formula for trapezoid area,  A = y(b + B)/2, is a good starting point for obtaining a useful equation for A.  It can be seen from the diagram that B = b + 2zy, so the trapezoid area can be expressed in terms y, b, and z:  A = (y/2)(b + b + 2zy)

Simplifying gives: A = by + zy2.

The wetted perimeter can be expressed as: P = b + 2λ.  The typically unknown sloped length, λ, can be eliminated using the Pythagoras Theorem:

λ2= y2+ (yz)2, or λ = [y2+ (yz)2]1/2 Thus the wetted perimeter is:

P = b + 2y(1 + z2)1/2,   and the hydraulic radius for a trapezoid can be calculated from:

R = (by + zy2)/[b + 2y(1 + z2)1/2]

Hydraulic Radius Open Channel Flow Triangular Flume Calculations

hydraulic radius open channel flow diagram for triangular channelAnother shape used in open channel flow is the triangular flume, as shown in the diagram at the right. The side slope is the same on both sides of the triangle in the diagram.  This is often the case.  The parameters used for hydraulic radius open channel flow calculations with a triangular flume are as follows:

  • B is the surface width of the liquid (ft for U.S. & m for S.I.)
  • λ is the sloped length of the triangle side (ft for U.S. & m for S.I.)
  • y is the liquid depth measured from the vertex of the triangle (ft for U.S. & m for S.I.)
  • z is the side slope specification in the form:  horiz:vert = z:1.

The common formula for triangle area is: A = By/2.  As shown in the figure, however,

B = 2yz, so the triangle area simplifies to: A = y2z.

The wetted perimeter is: P = 2λ , but as with the trapezoidal flume:  λ2= y2+ (yz)2.

This simplifies to the convenient equation: P = 2[y2(1 + z2)]1/2

The hydraulic radius is thus: RH= A/P = y2z/{2[y2(1 + z2)]1/2}

Excel Spreadsheets for Hydraulic Radius Open Channel Flow Calculations

With the equations given in the previous sections, the hydraulic radius can be calculated for a rectangular, triangular or trapezoidal flume if appropriate channel size/shape parameters are known along with the depth of flow.  An Excel spreadsheet like the one shown in the image below, however, can make the the calculations very conveniently.  Excel spreadsheets like the one shown below for use as hydraulic radius open channel flow calculators for rectangular, triangular, and trapezoidal flumes, as well as for partially full pipe flow, are available in our spreadsheet store.

screenshot of hydraulic radius open channel flow Excel spreadsheet

References:

1. Bengtson, Harlan H., Open Channel Flow I – The Manning Equation and Uniform Flow, an online, continuing education course for PDH credit.

2. U.S. Dept. of the Interior, Bureau of Reclamation, 2001 revised, 1997 third edition, Water Measurement Manual.

3. Chow, V. T., Open Channel Hydraulics, New York: McGraw-Hill, 1959.

4. Bengtson, Harlan H., “The Manning Equation for Open Channel Flow Calculations,” available as an Amazon Kindle e-book and as a paperback.