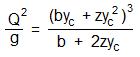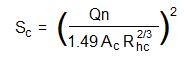Tag Archives: open channel flow

Hydraulic Jump Calculator Excel Spreadsheets

Posted on by
Reply

Where to Find Hydraulic Jump Calculator Excel Spreadsheets

For an Excel spreadsheets to use as an open channel flow, hydraulic jump calculator, click here to visit our spreadsheet store.  Obtain a convenient, easy to use rectangular channel hydraulic jump calculator spreadsheet for only $14.95. Read on for information about the use of an Excel spreadsheet as a horizontal, rectangular channel hydraulic jump calculator.

Background for Hydraulic Jump Calculator

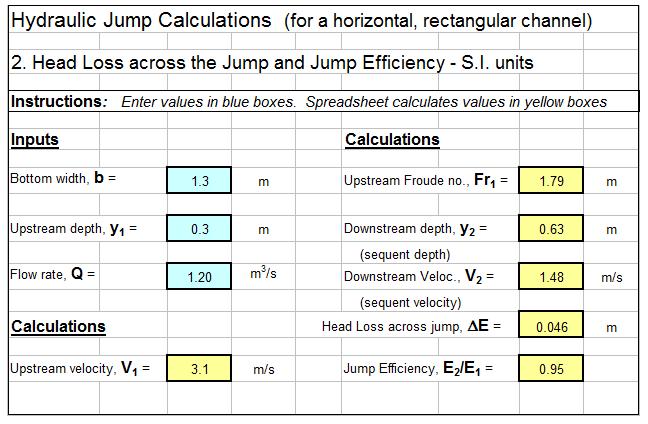
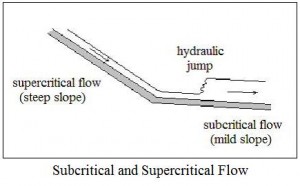In order to discuss hydraulic jumps it’s necessary to talk about subcritical and supercritical flow.  In general subcritical flow takes place at low velocities and high flow depths, while supercritical flow occurs at high velocities and low flow depths.  For more details about critical, subcritical, and supercritical flow, see the article, “Open Channel Flow Spreadsheets – Critical Depth and Critical Slope.”  The diagram above shows supercritical flow on a steep slope, changing to subcritical flow on a mild slope.  As shown, the transition from supercritical flow to subcritical flow takes place with a hydraulic jump.  Whenever supercritical flow takes place on a slope that isn’t steep enough to maintain supercritical flow, the transition to subcritical flow will take place through the mechanism of a hydraulic jump as illustrated in the diagram.

Hydraulic Jump Calculator Parameters

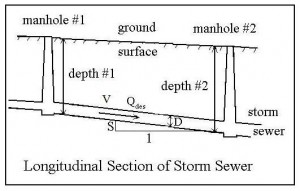
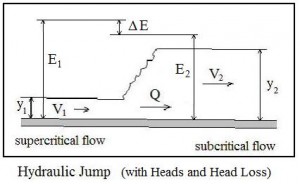Hydraulic jump calculations center on relationships among the supercritical conditions before the jump (upstream or initial conditions) and the subcritical conditions after the jump (downstream or sequent conditions).  The diagram at the left shows initial supercritical parameters and sequent subcritical parameters for a hydraulic jump.  The parameters and their typical units are summarized below:

  • y1 = the initial (upstream) depth of flow in ft for U.S. or m for S.I. units
  • V1 = the initial (upstream) liquid velocity in ft/sec for U.S. or m/s for S.I. units
  • E1 = the initial (upstream) head in ft for U.S. or m for S.I. units
  • y2 = the sequent (downstream) depth of flow in ft for U.S. or m for S.I. units
  • V2 = the sequent (downstream) liquid velocity in ft/sec for U.S. or m/s for S.I. units
  • E2 = the sequent (downstream) head in ft for U.S. or m for S.I. units
  • Q = the flow rate through the hydraulic jump in cfs for U.S. or m3/s for S.I. units
  • ΔE = the head loss across the hydraulic jump in ft for U.S. or m for S.I. units

An Excel Spreadsheet as a Hydraulic Jump Calculator

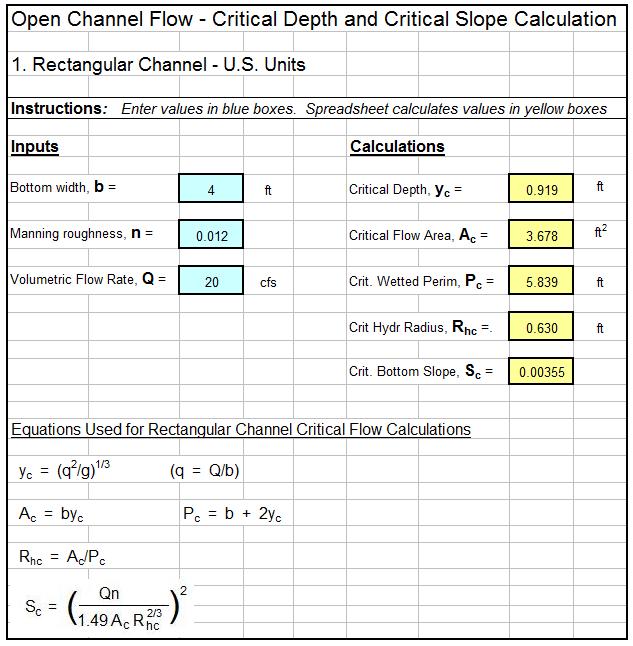
The Excel spreadsheet template shown below can be used to carry out hydraulic jump calculations.   Why bother to make these calculations by hand?  This Excel spreadsheet can calculate the sequent depth, sequent velocity, jump length, head loss across the jump, and hydraulic jump efficiency for specified initial depth, flow rate and channel width.  These spreadsheets are available in either U.S. or S.I. units at a very low cost (only $14.95 in our spreadsheet store.  These spreadsheets also have a tab for calculation of flow rate under a sluice gate and all of the equations used in the spreadsheet calculations are shown on the spreadsheets.

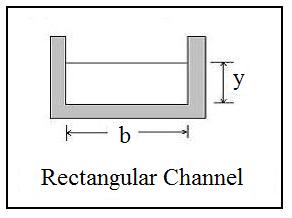
Note that some of the equations used in the spreadsheet calculations apply only for rectangular, horizontal channels, so the spreadsheets should be used only for channels that are at least approximately rectangular in cross-section and have a zero or very small slope.

References

1. Harlan H. Bengtson, “Hydraulic Jumps and Supercritical and Nonuniform Open Channel Flow,”  an online continuing education course for Professional Engineers.

2.  U.S. Department of Transportation, FHWA, Hydraulic Design of Energy Dissipators for Culverts and Channels, Hydraulic Engineering Circular No. 14, 3rd Ed, Chapter 6: Hydraulic Jump.

Critical Depth Open Channel Flow Spreadsheet

Posted on by
2

Where to Find a Critical Depth Open Channel Flow Spreadsheet

To obtain a critical depth open channel flow spreadsheet for calculating critical depth and/or critical slope for open channel flow, click here to visit our spreadsheet store.  Read on for information about the use of a critical depth open channel flow spreadsheet for critical depth and critical slope calculations.

The Froude Number and Critical, Subcritical and Supercritical Flow

Any particular example of open channel flow will be critical, subcritical, or supercritical flow.  In general, supercritical flow is characterized by high liquid velocity and shallow flow, while subcritical flow is characterized by low liquid velocity and relatively deep flow.  Critical flow is the dividing line flow condition between subcritical and supercritical flow.

The Froude number is a dimensionless number for open channel flow that provides information on whether a given flow is subcritical, supercritical or critical flow.  The Froude number is defined to be:  Fr = V/(gL)1/2 , where V is the average velocity, g is the acceleration due to gravity, and L is a characteristic length for the particular type of open channel flow.  For flow in a rectangular channel:  Fr = V/(gy)1/2 ,   where y is the depth of flow.  For flow in an open channel with a shape other than rectangular:  Fr = V/[g(A/B)]1/2 , where A is the cross-sectional area of flow, and B is the surface width.

The value of the Froude number for a particular open channel flow situation gives the following information:

  • For Fr < 1, the flow is subcritical
  • For Fr = 1, the flow is critical
  • For Fr > 1, the flow is supercritical

Calculation of Critical Depth

It is sometimes necessary to know the critical depth for a particular open channel flow situation.  This type of calculation can be done using the fact that Fr = 1 for critical flow.  It is quite straightforward for flow in a rectangular channel and a bit more difficult, but still manageable for flow in a non-rectangular channel.

For flow in a rectangular channel (using subscript c for critical flow conditions), Fr = 1 becomes:   Vc/(gyc)1/2 = 1.  Substituting Vc =  Q/Ac =  Q/byc and  q = Q/b  (where b = the width of the rectangular channel), and solving for yc gives the following equation for critical depth: yc =  (q2/g)1/3.   Thus, the critical depth can be calculated for a specified flow rate and rectangular channel width.

For flow in a trapezoidal channel, Fr = 1 becomes:  Vc/[g(A/B)c]1/2 = 1.  Substituting the equation above for Vc together with Ac =  yc(b + zyc)    and   Bc =  b  +  zyc2 leads to the following equation, which can be solved by an iterative process to find the critical depth:

Critical Depth Open Channel Flow Spreadsheet Formula1

Calculation of Critical Slope

After the critical depth, yc ,  has been determined, the critical slope, Sc , can be calculate using the Manning equation if the Manning roughness coefficient, n, is known.  The Manning equation can be rearranged as follows for this calculation:

Critical Depth Open Channel Flow Spreadsheet Formula2Note that Rhc , the critical hydraulic radius, is given by:

Rhc =  Ac/Pc,  where Pc =  b  +  2yc(1 + z2)1/2

Note that calculation of the critical slope is the same for a rectangular channel or a trapezoidal channel, after the critical depth has been determined.  The Manning equation is a dimensional equation, in which the following units must be used:  Q is in cfs, Ac is in ft2, Rhc is in ft, and Sc and n are dimensionless.

Calculations in S.I. Units

The equations for calculation of critical depth are the same for either U.S. or S.I. units.  All of the equations are dimensionally consistent, so it is just necessary to be sure that an internally consistent set of units is used.  For calculation of the critical slope, the S.I. version of the Manning equation must be used, giving:

Critical Depth Open Channel Flow Spreadsheet Formula4In this equation, the following units must be used:  Q is in m3/s, Ac is in m2, Rhc is in m, and Sc and n are dimensionless.

A Critical Depth Open Channel Flow Spreadsheet Screenshot

The critical depth open channel flow spreadsheet template shown below can be used to calculate the critical depth and critical slope for a rectangular channel with specified flow rate, bottom width, and Manning roughness coefficient.  Why bother to make these calculations by hand?  This Excel spreadsheet and others with similar calculations for a trapezoidal channel are available in either U.S. or S.I. units at a very low cost in our spreadsheet store.

Critical Depth Open Channel Flow Spreadsheet Screenshot

References

1. Munson, B. R., Young, D. F., & Okiishi, T. H., Fundamentals of Fluid Mechanics, 4th Ed., New York: John Wiley and Sons, Inc, 2002.

2. Chow, V. T., Open Channel Hydraulics, New York: McGraw-Hill, 1959.

3. Bengtson, Harlan H. Open Channel Flow II – Hydraulic Jumps and Supercritical and Nonuniform Flow – An online, continuing education course for PDH credit.

 

 

 

Storm Sewer Hydraulic Design with Excel Spreadsheets

Posted on by

Where to Find Storm Sewer Hydraulic Design Spreadsheets

For storm sewer hydraulic design spreadsheets, click here to visit our spreadsheet store.  Read on for information about the use of Excel spreadsheets for storm sewer hydraulic design calculations with the Manning Equation.

One part of storm sewer hydraulic design is determination of the design pipe diameter and sewer slope for the storm sewer pipe between adjacent manholes.  Although storm sewers are circular pipes, the storm water typically flows under gravity, rather than as pressure flow, so the Manning equation for open channel flow can be used for the calculations.  A storm sewer hydraulic design spreadsheet typically makes hydraulic calculations for full pipe flow.  For full pipe flow, the hydraulic radius becomes: R = A/P = (πD2/4)/(πD) = D/4.

The Manning Equation in a Storm Sewer Hydraulic Design Spreadsheet

The general form of the Manning equation in terms of velocity is: V = (1.49/n)(R2/3)(S1/2) for U.S. units and  V = (1.0/n)(R2/3)(S1/2) for S.I. units.  As noted above, R = D/4 for full pipe flow, so the Manning equation in U.S. units becomes  V = (1.49/n)[(D/4)2/3](S1/2) -U.S. units or V = (1.0/n)[(D/4)2/3](S1/2) – S.I units, for full pipe, gravity flow in a storm sewer pipe.  The parameters in the equations are as follows:

  • V is the flow velocity in the pipe (ft/sec – U.S. and m/s – S.I.).
  • n is the Manning roughness coefficient, an empirical, dimensionless constant.
  • D is the pipe diameter (ft -U.S. and m – S.I.).
  • S is the pipe slope, which is dimensionless.

The volumetric flow rate is related to the other parameters through the equation Q = VA or, for a circular pipe flowing full:  Q = (πD2/4)V, where Q will be in cfs for U.S. units or m3/s for S.I. units.

Calculation of Diameter and Slope with a Storm Sewer Hydraulic Design Spreadsheet

Diagram for Storm Sewer Hydraulic Design SpreadsheetThe required diameter and slope for the length of storm sewer between two manholes can be calculated with a storm hydraulic sewer design spreadsheet using the equations presented in the last section (Mannings equation and Q = VA) together with the typical design criteria that 1) the full pipe flow rate that the pipe can carry must be at least equal to the design peak storm water runoff rate to the inlet for that section of storm sewer and 2) the full pipe velocity must be equal to or greater than a specified minimum velocity.  The diagram above shows a sectional view of a storm sewer pipe between two manholes and the parameters being discussed here. The calculation procedure is illustrated by the example in the next section.

Example Storm Sewer Hydraulic Design Calculations

Problem Statement: For a section of storm sewer between two manholes, the design flowrate is: Qdes = 6.4 cfs. The required minimum full pipe storm water velocity is: V min= 3 ft/sec.  The Manning roughness coefficient (concrete pipe) is: n = 0.011.  Find a standard pipe diameter and sewer slope that will meet the two criteria: Qfull > Qdes and Vfull > Vmin for this section of storm sewer pipe.

Problem Solution: First the pipe diameter needed for a full pipe velocity of 3 ft/sec at design flow rate will be calculated using the equation: Q = VA.   Then the Manning equation will be used to calculate the sewer slope needed to give full pipe velocity equal to 3 ft/sec with the next larger standard pipe size.

Step 1:  The equation, Q = VA becomes: Qfull = Vfull(πD2/4). Substituting known values for Qfull and Vfull, the equation becomes: 6.4 = 3(πD2/4).  Solving for D gives: D = 1.65 ft = 19.8 in.  From the list of standard storm sewer pipe sizes in the next section it can be seen that the next standard size larger than 19.8 inches is 21 “, so that will be used for the diameter.

The Manning equation will then be used to calculate the slope for D = 21 in. = 1.75 ft, and V = 3 ft/sec. The Manning equation is: V = (1.49/n)[(D/4)2/3](S1/2).  Substituting values for V, D, and n gives:  3 = (1.49/0.011)[(1.75/4)2/3](S1/2).  Solving this equation for S gives: S = 0.00148.

Thus, the solution is: D = 21″, S = 0.00148. These values of D and S will give Qfull > 6.4 cfs, because Qfull = 6.4 cfs for Vfull = 3 ft/sec and D = 19.8″. With D = 21 ” and V = 3 ft/sec, Qfull must be greater than 6.4 cfs. The equation Q = (πD2/4)V can be used to check this.

Standard Pipe Sizes

Standard U.S. pipe sizes in inches for most types of pipe used as storm sewers:                          4, 6, 8, 10, 12, 14, 16, 18, 21, 24, 27, 30, 33, 36, 39, 42, 48, 54, 60

Standard S.I. pipe sizes in mm for most types of pipe used as storm sewers:                           100, 150, 200, 250, 300, 350, 400, 450, 500, 600, 650, 700, 750, 800, 850, 900, 950, 1000, 1050

Use of Excel Spreadsheets for Storm Sewer Design Calculations

For information on making storm sewer calculations with Excel spreadsheets, see the related article: “Excel Spreadsheets for Storm Sewer Hydraulic Design.”  For low cost, easy to use spreadsheets for several types of storm water calculations, including storm sewer hydraulic design, click here to visit our spreadsheet store.

References

1. Bengtson, Harlan H., Hydraulic Design of Storm Sewers, Including the Use of Excel, an online, continuing education course for PDH credit.

2. McCuen, Richard H., Hydrologic Analysis and Design, 2nd Ed, Upper Saddle River, NJ, Prentice Hall, 1998.

3. Steele, E.W. and McGhee, T.J., Water Supply and Sewerage, New York, NY, McGraw-Hill Book Co, 1979.

4. Bengtson, Harlan H., Hydraulic Design of Storm Sewers with a Spreadsheet,” an Amazon Kindle ebook

5. Bengtson, Harlan H., “Hydraulic Design of Storm Sewers with Excel”  an online blog article.

 

 

Hydraulic Radius Open Channel Flow Excel Spreadsheets

Posted on by

Where to Find Spreadsheets for Hydraulic Radius Open Channel Flow Calculations

For an Excel spreadsheet to use for hydraulic radius open channel flow calculations, click here to visit our spreadsheet store.  Read on for information about hydraulic radius open channel flow calculations.

The hydraulic radius is an important parameter for open channel flow calculations with the Manning Equation.  Excel spreadsheets can be set up to conveniently make hydraulic radius open channel flow calculations for flow through common open channel shapes like those for a rectangular, triangular or trapezoidal flume.  Parameters like trapezoid area and perimeter and triangle area and perimeter are needed to calculate the hydraulic radius as described in the rest of this article.

The hydraulic radius for open channel flow is defined to be the cross sectional area of flow divided by the wetted perimeter.  That is: R = A/P, where A is the cross sectional area of flow, P is the portion of the cross sectional perimeter that is wetted by the flow, and R is the hydraulic radius.  The next several sections will present the equations to calculate A, P, and R for some common open channel shapes, and then discuss the use of Excel spreadsheets for hydraulic radius open channel flow calculations.

Hydraulic Radius Open Channel Flow Calculation for Rectangular Channels

hydraulic radius open channel flow diagram for rectangular channelRectangular channels are widely used for open channel flow, and hydraulic radius open channel flow calculations are quite straightforward for a rectangular cross section. The diagram at the left shows the depth of flow represented by the symbol, y, and the channel bottom width represented by the symbol, b.  It is clear from the diagram that A = by and P = 2y + b.  Thus the equation for the hydraulic radius is: R = by/(2y + b) for open channel flow through a rectangular cross section.


Hydraulic Radius Open Channel Flow Trapezoidal Flume Calculations

hydraulic radius open channel flow diagram for trapezoidal flumeThe trapezoid is probably the most common shape for open channel flow. Many man-made open channels are trapezoidal flumes, including many urban storm water arroyos in the southwestern U.S.  Also, many natural channels are approximately trapezoidal in cross section. The parameters typically used for the size and shape of a trapezoidal flume in hydraulic radius open channel flow calculations are shown in the diagram at the right. Those parameters, which are used to calculate the trapezoid area and wetted perimeter, are as follows:

  • y is the liquid depth (ft for U.S. & m for S.I.)
  • b is the bottom width of the channel (ft for U.S. & m for S.I.)
  • B is the width of the liquid surface (ft for U.S. & m for S.I.)
  • λ is the wetted length measured along the sloped side (ft for U.S. & m for S.I.)
  • α is the angle of the sloped side from vertical. The side slope also often specified as horiz:vert = z:1.

The common formula for trapezoid area,  A = y(b + B)/2, is a good starting point for obtaining a useful equation for A.  It can be seen from the diagram that B = b + 2zy, so the trapezoid area can be expressed in terms y, b, and z:  A = (y/2)(b + b + 2zy)

Simplifying gives: A = by + zy2.

The wetted perimeter can be expressed as: P = b + 2λ.  The typically unknown sloped length, λ, can be eliminated using the Pythagoras Theorem:

λ2= y2+ (yz)2, or λ = [y2+ (yz)2]1/2 Thus the wetted perimeter is:

P = b + 2y(1 + z2)1/2,   and the hydraulic radius for a trapezoid can be calculated from:

R = (by + zy2)/[b + 2y(1 + z2)1/2]

Hydraulic Radius Open Channel Flow Triangular Flume Calculations

hydraulic radius open channel flow diagram for triangular channelAnother shape used in open channel flow is the triangular flume, as shown in the diagram at the right. The side slope is the same on both sides of the triangle in the diagram.  This is often the case.  The parameters used for hydraulic radius open channel flow calculations with a triangular flume are as follows:

  • B is the surface width of the liquid (ft for U.S. & m for S.I.)
  • λ is the sloped length of the triangle side (ft for U.S. & m for S.I.)
  • y is the liquid depth measured from the vertex of the triangle (ft for U.S. & m for S.I.)
  • z is the side slope specification in the form:  horiz:vert = z:1.

The common formula for triangle area is: A = By/2.  As shown in the figure, however,

B = 2yz, so the triangle area simplifies to: A = y2z.

The wetted perimeter is: P = 2λ , but as with the trapezoidal flume:  λ2= y2+ (yz)2.

This simplifies to the convenient equation: P = 2[y2(1 + z2)]1/2

The hydraulic radius is thus: RH= A/P = y2z/{2[y2(1 + z2)]1/2}

Excel Spreadsheets for Hydraulic Radius Open Channel Flow Calculations

With the equations given in the previous sections, the hydraulic radius can be calculated for a rectangular, triangular or trapezoidal flume if appropriate channel size/shape parameters are known along with the depth of flow.  An Excel spreadsheet like the one shown in the image below, however, can make the the calculations very conveniently.  Excel spreadsheets like the one shown below for use as hydraulic radius open channel flow calculators for rectangular, triangular, and trapezoidal flumes, as well as for partially full pipe flow, are available in our spreadsheet store.

screenshot of hydraulic radius open channel flow Excel spreadsheet

References:

1. Bengtson, Harlan H., Open Channel Flow I – The Manning Equation and Uniform Flow, an online, continuing education course for PDH credit.

2. U.S. Dept. of the Interior, Bureau of Reclamation, 2001 revised, 1997 third edition, Water Measurement Manual.

3. Chow, V. T., Open Channel Hydraulics, New York: McGraw-Hill, 1959.

4. Bengtson, Harlan H., “The Manning Equation for Open Channel Flow Calculations,” available as an Amazon Kindle e-book and as a paperback.