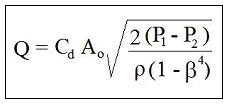Tag Archives: Reynolds number

Air Viscosity Temperature Calculator Spreadsheet

Posted on by
Reply

Where to Find an Air Viscosity Temperature Calculator Spreadsheet

To obtain an Air Viscosity Temperature Calculator excel spreadsheet, click here to visit our spreadsheet store.  Why use online calculators or tables to find the viscosity of air at a specified pressure and temperature when you can buy a convenient air viscosity temperature calculator excel spreadsheet for only $4.95?  This spreadsheet will calculate the viscosity of air at specified pressure and temperature in either U.S. or S.I. units.  Read on for information about Excel spreadsheets that can be used as an Air viscosity temperature calculator for specified pressure and temperature.

Air Viscosity Temperature Calculator Spreadsheet Applications

An  Air Viscosity Temperature calculator excel spreadsheet  can be used for any situation where a value of air viscosity is needed at a specified pressure and temperature.  This could include calculations for air flow in a pipe, drag force or drag coefficient calculations for flow of an object through air, and any other calculation requiring the Reynolds number for air flow or flow through air.  For example, see the related article, Fanno Flow Excel Spreadsheet for Air Flow in a Pipe.

Equations for an Air Viscosity Temperature Calculator Spreadsheet

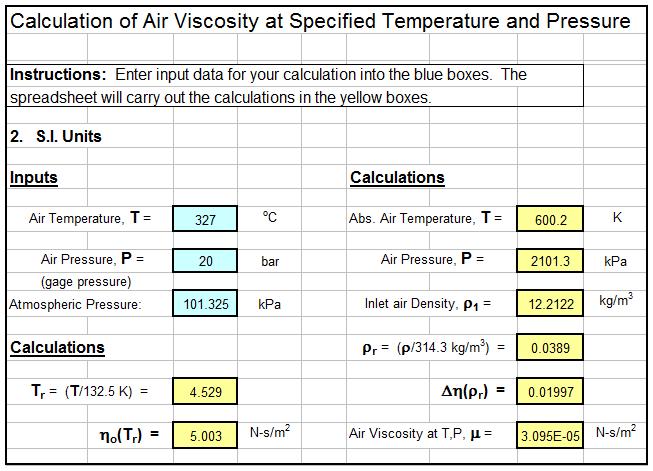
Equations are available for an air viscosity temperature calculator to calculate the viscosity of air at specified temperature and pressure.  The spreadsheet shown in  the diagram below calculates air density using an equation for air viscosity as a function of temperature ratio, Tr , and density ratio, ρr  , where in U.S. units:  Tr   =  T/238.5 with T in degrees R  and ρr    =  ρ/0.6096 with ρ in slugs/ft3.  Since the air density is needed for this calculation, the spreadsheet also calculates the density of air at the specified air temperature and pressure.  The complete equations are included in the spreadsheet discussed above and shown in the screenshot below.

Example Air Viscosity Temperature Calculator Excel Spreadsheet

The Air Viscosity Temperature calculator excel spreadsheet shown in the image below can be used to calculate the viscosity of air at given temperature and pressure as discussed above.  This Excel spreadsheet and others for fluid properties calculations, in either U.S. or S.I. units are available for very reasonable prices in our spreadsheet store.

Air Viscosity Temperature Calculator Spreadsheet

References

1. Bengtson, Harlan H, “Air Viscosity Calculator Pressure Temperature Spreadsheet,”  An online informational blog article.

Orifice and Venturi Flow Meter Calculations Spreadsheet

Posted on by

Introduction to Orifice and Venturi Flow Meter Calculations Spreadsheet

For an orifice and venturi flow meter calculations spreadsheet, click here to visit our spreadsheet store.  Read on for information about Excel spreadsheets that can be used as orifice and venturi flow meter, pipe flow rate calculators.

Excel spreadsheets are convenient for differential pressure flow meter calculations,  for meters such as the commonly used orifice flow meter and venturi meter.  The general equation for differential pressure flow meters can be built into the spreadsheets with Excel formulas.  Also, for gas flow, the ideal gas law can be used to calculate the gas density based on its temperature, pressure, and molecular weight.  An Excel spreadsheet can also be used to calculate the orifice coefficient for anorifice meter with one of the ISO standard pressure tap configurations.

Background for an Orifice and Venturi Flow Meter Calculation Spreadsheet

Orifice and Venturi Flow Meter Calculations Spreadsheet diagramOrifice and venturi meters both function by sending pipe flow through a constricted area (the orifice plate or the venturi throat), as shown in the diagrams at the right.  Due to the increased fluid velocity passing through the constriction, there will be a decreased pressure at that location.   The pipe flow rate can then be calculated from the measured pressure difference between the undisturbed pipe flow and the flow through the constriction.

The general equation for calculating fOrifice and Venturi Flow Meter Calculations Spreadsheet Equationlow rate through either an orifice or venturi meter is shown at the left, where the parameters in the equation and their units are as follows:

 

  • Q is the flow rate through the pipe and through the meter  (cfs – U.S. or m3/s – S.I.)
  • Cd is the discharge coefficient, which is dimensionless
  • Ao is the constricted area perpendicular to flow  (ft2 – U.S. or m2 – S.I.)
  • P1 is the undisturbed upstream pressure in the pipe  (lb/ft2 – U.S. or N/m2 – S.I.)
  • P2 is the pressure in the pipe at the constricted area, Ao (lb/ft2 – U.S. or N/m2 – S.I.)
  • β = D2/D1 = (diam. at A2/pipe diam.), which is dimensionless
  • ρ is the fluid density (slugs/ft3 – U.S. or kg/m3 – S.I.)

Orifice and Venturi Flow Meter Calculations Spreadsheet Screenshot

The image below shows an Excel spreadsheet that can be used as a pipe flow rate calculator, based on the measured pressure difference across a flow nozzle, venturi, or Orifice flow meter.  This spreadsheet is suitable when the fluid density is known (as for a liquid) and the meter coefficient, C, is known.  For this spreadsheet and another to calculate the density of a gas using the ideal gas law model, click here to visit our spreadsheet store.

Orifice and Venturi Flow Meter Calculations Spreadsheet ScreenshotReferences

1. Munson, B. R., Young, D. F., & Okiishi, T. H., Fundamentals of Fluid Mechanics, 4th Ed., New York: John Wiley and Sons, Inc, 2002.

2. U.S. Dept. of the Interior, Bureau of Reclamation, 2001 revised, 1997 third edition, Water Measurement Manual, available for on-line use or download at: http://www.usbr.gov/pmts/hydraulics_lab/pubs/wmm/index.htm

3. International Organization of Standards – ISO 5167-1:2003 Measurement of fluid flow by means of pressure differential devices, Part 1: Orifice plates, nozzles, and Venturi tubes inserted in circular cross-section conduits running full. Reference number: ISO 5167-1:2003.

4. Bengtson, Harlan H., “Orifice and Venturi Flow Meters: for Liquid Flow and Gas Flow.” an Amazon Kindle e-book.

Forced Convection Heat Transfer Coefficient Calculator

Posted on by

Where to Find a Forced Convection Heat Transfer Coefficient Calculator Spreadsheet

For an Excel spreadsheet to use as a forced convection heat transfer coefficient calculator, click here to visit our spreadsheet store.  Read on for information about forced convection heat transfer coefficients and their calculation.

An Excel spreadsheet can be a convenient forced convection heat transfer coefficient calculator.   This type of calculation is typically based on a correlation of dimensionless numbers, usually Nusselt number in terms of Reynolds number and Prandtl number.  Forced convection occurs with a fluid moving past a solid surface when the fluid and the solid are at different temperatures.  Newton’s Law of Cooling [ Q = hA(Ts – Tf) ] is a simple expression for the rate for convective heat transfer.  The parameters in Newton’s Law of Cooling are:

  • Q is the rate of forced convection heat transfer (Btu/hr – U.S. or W – S.I.)
  • Ts is the solid temperature (oF – U.S. or oC – S.I.)
  • Tf is the fluid temperature (oF – U.S. or oC – S.I.)
  • A is the area of the surface that is in contact with the fluid (ft2 – U.S. or m2 – S.I.)
  • h is the convective heat transfer coefficient (Btu/hr-ft2–oF – U.S. or W/m2-K – S.I.)

Dimensionless Numbers for a Forced Convection Heat Transfer Coefficient Calculator

Determining a good estimate for the heat transfer coefficient, h, is often the most difficult part of forced convection heat transfer calculations.  The process for estimating the heat transfer coefficient for a particular forced convection application is often through a correlation for Nusselt number (Nu) in terms of Reynolds number (Re) and Prandtl number (Pr).  These three dimensionless numbers are defined in the box below, along with the definitions of the parameters that appear in them.

Forced Convection Heat Transfer Coefficient Calculator Dimensionless Numbers

Nusselt Number Correlations for Turbulent Flow Inside a Pipe

The Dittus Boelter equation, which has been around since 1930 (ref #1) has two forms as follows:

Nuo = 0.023 Re0.8Pr0.4 , for ‘heating’ (temperature of wall > temperature of fluid), and

Nuo = 0.026 Re0.8Pr0.3 , for ‘cooling’ (temperature of wall < temperature of fluid).

Subject to: 0.7 < Pr < 120 ; 10,000 < Re < 160,000; L/D > 10 ( L/D > 50 according to some authors).  It is a rather simple equation to use, but has a fairly narrow range of acceptable values for Re and Pr.

Forced Convection Heat Transfer Coefficient Calculator Nusselt Number CorrelationsAnother correlation (from ref #2) is shown in the box at the right.  The range of values for Re and Pr for this correlation are also shown.  This correlation can be used for a wider range of values of Re and Pr.

A third correlation is shown in the box at the left below.  This correlation, described by Pethukov (ref #3) is only a minor variation of the second correlation shown at the right.  This third correlation works for an even wider range of values for Re and Pr.

Nusselt Number Correlation for Forced Convection Heat Transfer Coefficient CalculatorExcel spreadsheets can be conveniently used as a forced convection heat transfer coefficient calculator with correlations like these or others for configurations like laminar pipe flow, flow inside a circular annulus, flow outside a cylinder, flow past a bank of tubes, or flow in a noncircular cylinder, because the equations can be programmed into the spreadsheet using Excel formulas.  For free download of an Excel spreadsheet for calculating forced convection heat transfer coefficients for laminar pipe flow, and low cost spreadsheets for all of the other configurations mentioned above,  click here to visit our spreadsheet store.

References

1.  Dittus, P.W. and Boelter, L.M., Univ. Calif. Pub. Eng., Vol. 1, No. 13, pp 443-461 (reprinted in Int. Comm. Heat Mass Transfer, Vol. 12, pp 3-22 (1985).

2.  egr.msu.edu

3.  Petukhov, B.S., “Heat transfer and friction in turbulent pipe flow with variable physical properties,” Adv. Heat Transfer 6, 503-565 (1970).