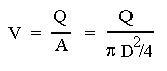S.I. units Archives - Page 4 of 4 - Low Cost Easy to Use Spreadsheets for Engineering Calculations Available at Engineering Excel SpreadsheetsLow Cost Easy to Use Spreadsheets for Engineering Calculations Available at Engineering Excel Spreadsheets

Where to Find a Pipe Flow-Friction Factor Calculator Excel Spreadsheet

For a pipe flow-friction factor calculator Excel Spreadsheet, click here to visit our spreadsheet store. Why read values from a Moody diagram, make iterative calculations to get friction factor, or use online calculators, when you can get a pipe flow-friction factor calculator Excel Spreadsheet for only $19.95? Read on for information about the Darcy Weisbach equation and its use in an Excel spreadsheet as a friction factor/pipe flow calculator.

Excel spreadsheets are very convenient for Darcy Weisbach equation/pipe flow calculations, such as frictional pressure drop calculation or use of a friction factor calculator, at least in part because some of the calculations require iterative solutions. The Darcy Weisbach equation is applicable to pressure flow in pipes, rather than gravity flow (as in sewer pipes), which is handled by open channel flow equations like the Manning equation. The Darcy Weisbach equation provides the relationship among the following parameters: pipe diameter and length, pipe flow rate, and frictional pressure drop or head loss. Any one of these can be calculated if the others are known along with the density and viscosity of the fluid.

A Friction Factor Calculator and the Darcy Weisbach Equation

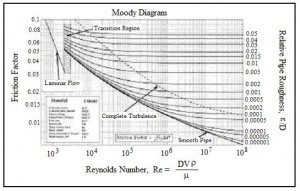The Darcy Weisbach equation is h_L= f(L/D)(V²/2g), with the parameters in the equation as follows: h_Lis the frictional head loss for flow of a fluid at average velocity, V, through a pipe of length,L, and diameter,D. The Reynolds number for the flow (Re) and the relative roughness of the pipe (e/D) are needed to get a value for the friction factor,f. The Moody Diagram at the right shows the nature of the dependence of the friction factor, f, on Re and e/D.

Equations for f as a function of Re and e/D would be more convenient than a graph like the Moody Diagram for use with Excel spreadsheets making pipe flow calculations with the Darcy Weisbach equation. Such equations are shown in the box at the left, giving the relationships between Moody friction factor and Re & e/D for four different portions of the Moody diagram. The four portions of the Moody diagram are:

laminar flow(Re < 2100 – the straight line at the left side of the Moody

smooth pipe turbulent flow(the dark curve labeled “smooth pipe” in the Moody diagram – f is a function of Re only in this region)
completely turbulent region(the portion of the diagram above and to the right of the dashed line labeled “complete turbulence” – f is a function of e/D only in this region)
transition region(the portion of the diagram between the “smooth pipe” solid line and the “complete turbulence” dashed line – f is a function of both Re and e/D in this region and this is not an explicit equation for f)

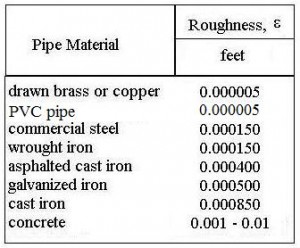
The table above right gives pipe roughness values for several common pipe materials. These can be used to calculate the pipe roughness ratio, e/D.

For a low cost Moody friction factor calculator download, that will calculate f for Reynolds number above 2100, see: www.engineeringexceltemplates.com

Frictional Head Loss and Frictional Pressure Drop Calculation

After using the Moody friction factor calculator to get a value for the friction factor, f, frictional head loss calculation is quite straightforward if the pipe length & diameter and average flow velocity are known. You simply need to substitute values for L, D, V, and f into the Darcy Weisbach equation [h_L= f(L/D)(V²/2g) ]. The Darcy Weisbach equation is a dimensionally consistent equation, so any consistent set of units can be used. For U.S. units, h_L, L, and D are typically in ft, V is in ft/sec, and g is 32.2 ft/sec². For S.I. units, h_L, L and D are typically in m, V is in m/s, and g is 9.81 m/s². If volumetric flow rate, Q, is known rather than average velocity, V, then V can be calculated from:

Frictional pressure drop calculation from frictional head loss is done through the equation:

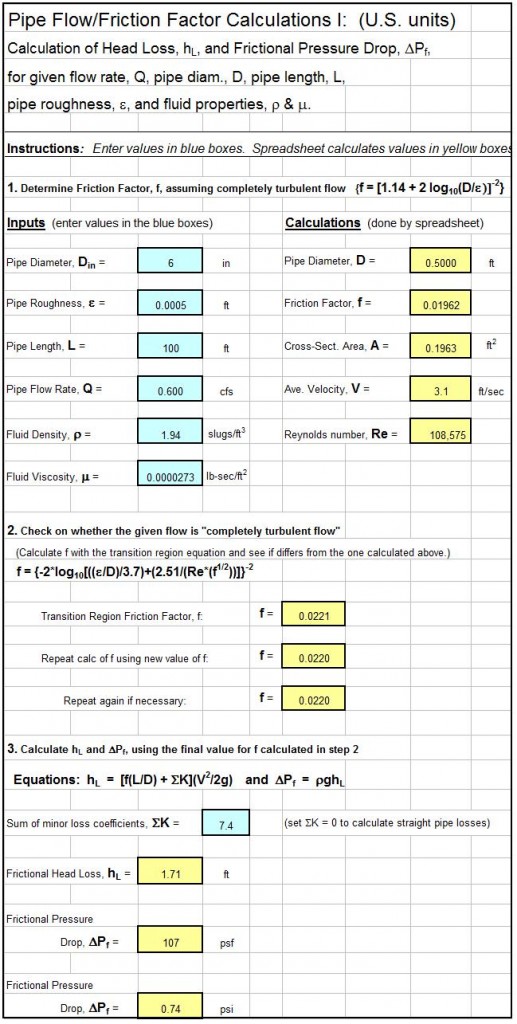
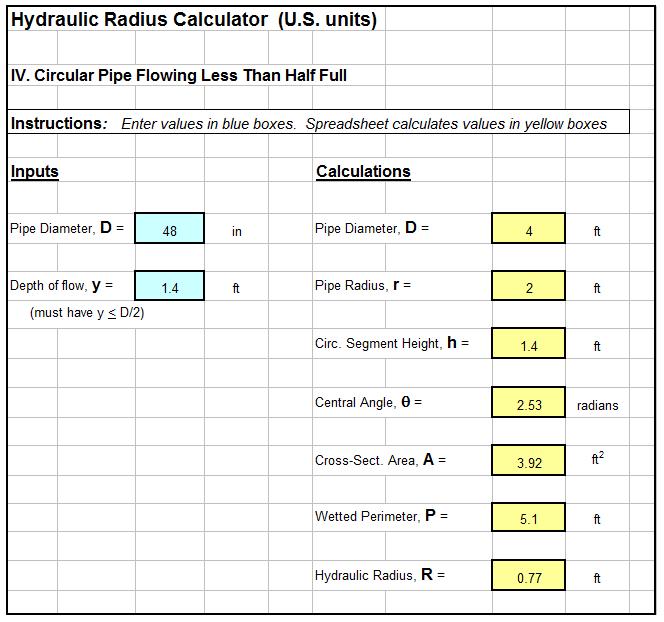
A Screenshot for a Pipe Flow-Friction Factor Calculator Excel Spreadsheet

The Excel spreadsheet screenshot below shows a pipe flow-friction factor calculator excel spreadsheet that is available as part of the “Pipe Flow-Friction Factor Calculation Package,” at our spreadsheet store in either U.S. or S.I. units at a very low cost (only $16.95). This spreadsheet package has three worksheets: one to calculate frictional head loss and pressure drop for known pipe diameter, length & material and flow rate; one to serve as a pipe flow rate calculator for known head loss/pressure drop, and pipe diameter, length & material; and one to calculate required pipe diameter for known head loss/pressure drop, flow rate, and pipe length & material.

References

1. Munson, B. R., Young, D. F., & Okiishi, T. H., Fundamentals of Fluid Mechanics, 4th Ed., New York: John Wiley and Sons, Inc, 2002.

2. Darcy Weisbach equation history – http://biosystems.okstate.edu/darcy/DarcyWeisbach/Darcy-WeisbachHistory.htm

3. Source for pipe roughness values – http://www.efunda.com/formulae/fluids/roughness.cfm

4. Bengtson, H.H., Pipe Flow/Friction Factor Calculations with Excel, and online continuing education course for Professional Engineers.

5. Bengtson, Harlan H., “Pipe Flow Friction Factor Calculations with Spreadsheets,” available as an Amazon Kindle e-book and as a paperback.

6. Bengtson, Harlan H., “Pipe Flow Calculations with the Darcy Weisbach Equation“, an online blog article

Where to Find Spreadsheets for Hydraulic Radius Open Channel Flow Calculations

For an Excel spreadsheet to use for hydraulic radius open channel flow calculations, click here to visit our spreadsheet store. Read on for information about hydraulic radius open channel flow calculations.

The hydraulic radius is an important parameter for open channel flow calculations with the Manning Equation. Excel spreadsheets can be set up to conveniently make hydraulic radius open channel flow calculations for flow through common open channel shapes like those for a rectangular, triangular or trapezoidal flume. Parameters like trapezoid area and perimeter and triangle area and perimeter are needed to calculate the hydraulic radius as described in the rest of this article.

The hydraulic radius for open channel flow is defined to be the cross sectional area of flow divided by the wetted perimeter. That is: R = A/P, where A is the cross sectional area of flow, P is the portion of the cross sectional perimeter that is wetted by the flow, and R is the hydraulic radius. The next several sections will present the equations to calculate A, P, and R for some common open channel shapes, and then discuss the use of Excel spreadsheets for hydraulic radius open channel flow calculations.

Hydraulic Radius Open Channel Flow Calculation for Rectangular Channels

Rectangular channels are widely used for open channel flow, and hydraulic radius open channel flow calculations are quite straightforward for a rectangular cross section. The diagram at the left shows the depth of flow represented by the symbol, y, and the channel bottom width represented by the symbol, b. It is clear from the diagram that A = by and P = 2y + b. Thus the equation for the hydraulic radius is: R = by/(2y + b) for open channel flow through a rectangular cross section.

Hydraulic Radius Open Channel Flow Trapezoidal Flume Calculations

The trapezoid is probably the most common shape for open channel flow. Many man-made open channels are trapezoidal flumes, including many urban storm water arroyos in the southwestern U.S. Also, many natural channels are approximately trapezoidal in cross section. The parameters typically used for the size and shape of a trapezoidal flume in hydraulic radius open channel flow calculations are shown in the diagram at the right. Those parameters, which are used to calculate the trapezoid area and wetted perimeter, are as follows:

y is the liquid depth (ft for U.S. & m for S.I.)
b is the bottom width of the channel (ft for U.S. & m for S.I.)
B is the width of the liquid surface (ft for U.S. & m for S.I.)
λ is the wetted length measured along the sloped side (ft for U.S. & m for S.I.)
α is the angle of the sloped side from vertical. The side slope also often specified as horiz:vert = z:1.

The common formula for trapezoid area, A = y(b + B)/2, is a good starting point for obtaining a useful equation for A. It can be seen from the diagram that B = b + 2zy, so the trapezoid area can be expressed in terms y, b, and z: A = (y/2)(b + b + 2zy)

Simplifying gives: A = by + zy².

The wetted perimeter can be expressed as: P = b + 2λ. The typically unknown sloped length, λ, can be eliminated using the Pythagoras Theorem:

λ²= y²+ (yz)², or λ = [y²+ (yz)²]^1/2 Thus the wetted perimeter is:

P = b + 2y(1 + z²)^1/2, and the hydraulic radius for a trapezoid can be calculated from:

R = (by + zy²)/[b + 2y(1 + z²)^1/2]

Hydraulic Radius Open Channel Flow Triangular Flume Calculations

Another shape used in open channel flow is the triangular flume, as shown in the diagram at the right. The side slope is the same on both sides of the triangle in the diagram. This is often the case. The parameters used for hydraulic radius open channel flow calculations with a triangular flume are as follows:

B is the surface width of the liquid (ft for U.S. & m for S.I.)
λ is the sloped length of the triangle side (ft for U.S. & m for S.I.)
y is the liquid depth measured from the vertex of the triangle (ft for U.S. & m for S.I.)
z is the side slope specification in the form: horiz:vert = z:1.

The common formula for triangle area is: A = By/2. As shown in the figure, however,

B = 2yz, so the triangle area simplifies to: A = y²z.

The wetted perimeter is: P = 2λ , but as with the trapezoidal flume: λ²= y²+ (yz)².

This simplifies to the convenient equation: P = 2[y²(1 + z²)]^1/2

The hydraulic radius is thus: R_H= A/P = y²z/{2[y²(1 + z²)]^1/2}

Excel Spreadsheets for Hydraulic Radius Open Channel Flow Calculations

With the equations given in the previous sections, the hydraulic radius can be calculated for a rectangular, triangular or trapezoidal flume if appropriate channel size/shape parameters are known along with the depth of flow. An Excel spreadsheet like the one shown in the image below, however, can make the the calculations very conveniently. Excel spreadsheets like the one shown below for use as hydraulic radius open channel flow calculators for rectangular, triangular, and trapezoidal flumes, as well as for partially full pipe flow, are available in our spreadsheet store.

References:

1. Bengtson, Harlan H., Open Channel Flow I – The Manning Equation and Uniform Flow, an online, continuing education course for PDH credit.

2. U.S. Dept. of the Interior, Bureau of Reclamation, 2001 revised, 1997 third edition, Water Measurement Manual.

3. Chow, V. T., Open Channel Hydraulics, New York: McGraw-Hill, 1959.

4. Bengtson, Harlan H., “The Manning Equation for Open Channel Flow Calculations,” available as an Amazon Kindle e-book and as a paperback.

Low Cost Easy to Use Spreadsheets for Engineering Calculations Available at Engineering Excel Spreadsheets

At Engineering Excel Spreadsheets, we have low cost, easy to use spreadsheets for engineering calculations, including pipe flow, flow measurement, stormwater measurement, heat transfer coefficients, open channel flow, structural analysis of beams, and more.

Tag Archives: S.I. units

Pipe Flow-Friction Factor Calculator Excel Spreadsheet